Dynamic programming is a term that has likely been thrown around by now if you’ve been in the field for any length of time. The topic comes up frequently in design review meetings and in engineers’ day-to-day interactions, and it is also a focal point in technical interviews. The divide-and-conquer strategy is a foolproof method for achieving any goal. In computer programming, this same idea is true. Numerous difficulties have subtypes that can be isolated and treated separately, allowing for the ultimate resolution of the primary issue. In this article, we will discuss the dynamic programming algorithm and Python.
What Is Dynamic Programming?
Dynamic programming is a method for solving complex issues by first reducing them to simpler ones, then using the solutions to those simpler problems as building blocks to solve the original problem.
We segment the issue at hand into manageable chunks. In most cases, the only real distinction between the parent’s problem and its child’s problems is their relative sizes. Thus, these mini-problems can be broken down into even more mini-problems, and so on, indefinitely. Imagine that an issue and its various subproblems form a tree. The “leaf” problems are tackled first, followed by their “parent” problems, and so on up the problem tree. As we tackle smaller difficulties, we record our progress for later use. This allows us to skip over that part of the problem in the future.
This method is similar to the divide and conquer technique in that it breaks a problem down into smaller problems that can be solved independently and then combined to obtain the final solution.
How Does Dynamic Programming Work?
Dynamic programming is effective because it simplifies difficult issues by decomposing them into constituent parts. The next step is to pinpoint the best answers to these ensuing challenges. The results of these procedures can be memorized so that the corresponding solutions can be retrieved from storage and used without further computation. Also, the solution can be saved to avoid recalculating previously solved subproblems.
Two methods exist for accomplishing dynamic programming:
#1. Top-Down Approach
In computer science, problems are typically solved by constructing solutions recursively, or by using the results of previous steps to tackle the problem at hand. It is possible to memorize or keep a table of the solutions to the subproblems if they are similar. The top-down method is based on learning by rote memory. Memoization is the same as performing recursion and caching twice. Recursion involves making an indirect call to the function, while caching involves keeping track of intermediate results.
Among the many advantages of the top-down approach are:
- The top-down method is simple to grasp and apply. To better understand what needs to be done, this method deconstructs problems into their component elements. Every new development brings with it the relief of a previously insurmountable obstacle. Some of the pieces may even be applicable to other problems.
- It enables the solution of subproblems on demand. The top-down method will allow for the decomposition of issues into manageable chunks, with the solutions to those chunks being stored for later use. Then, customers can ask for help with fixing each component.
- Debugging is also simplified. Dividing a problem into smaller chunks makes it easier to follow the answer and see potential mistakes.
The following are some of the drawbacks of using a top-down approach:
- The top-down strategy makes use of the recursion method, which takes up more memory in the call stack than other approaches. This ultimately results in a decrease in performance. In addition, a stack overflow can occur if the recursion goes too far back into the past.
#2. Bottom-Up Approach
After an issue’s solution has been expressed in terms of its subproblems in a fashion that loops back on itself, users can rewrite the problem using the bottom-up approach, in which they solve the smaller subproblems first and then apply their solutions to the bigger ones.
In contrast to the top-down method, the recursion is eliminated when using the bottom-up method. Therefore, the recursive functions do not add unnecessary overhead or cause the stack to overflow. In addition, it enables data compression. The temporal complexity of recursion is reduced by eliminating the need to recalculate the same values.
Some benefits of working from the ground up are as follows:
- It first determines how a huge problem will be constructed out of smaller, reusable subproblems.
- By doing away with recursion, it helps make better use of available memory. The timing complexity is reduced as a side effect.
Characteristics of Dynamic Programming
There are two distinguishing characteristics of dynamic programming:
#1. Subproblems Overlap
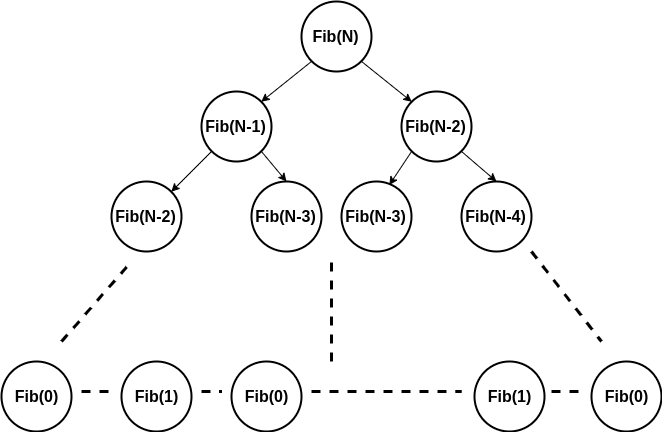
Modifications of a primary problem that are more manageable are called “subproblems.” The Fibonacci sequence, in which each number equals the sum of the two preceding ones (0, 1, 1, 2, 3, 5, 8,…). You can divide the task of finding the nth value in the Fibonacci sequence into more manageable chunks. As you find solutions by tackling the same subproblem over and over, these overlapping sets of difficulties become increasingly difficult to solve.
Dynamic programming can be used to partition large programming jobs into manageable chunks due to the universal occurrence of overlapping subproblems.
#2. Substructure Has Optimal Property
The property of optimum substructure manifests itself when it is possible to create an optimal solution from the solutions to all the subproblems. In order for recursion to work, you must apply the answer you derive from each overlap to the entire problem. The optimal substructure property is displayed by the whole problem when, as in the case of the Fibonacci sequence, each subproblem has a solution that can be applied to the next subproblem in the sequence to determine its value.
Uses of Dynamic Programming in the Real World
Here are the uses of dynamic programming.
#1. Knapsack Problem
Dynamic programming has been used extensively to solve the knapsack problem. These are the issues we’re facing:
The ideal value for each sub-issue, determined by the number of items in question and the amount of space left in the knapsack, can be stored in a two-dimensional array, making quick work of this problem. We can maximize value by including or excluding the current item at each stage. The answer can be found in the array’s lower-right corner.
The knapsack problem can be used in a wide variety of contexts, from packing luggage to making investment decisions to allocating resources.
#2. All Pair Shortest Path
The shortest path issue in a weighted graph is another typical use of dynamic programming. Using techniques like Floyd-Warshall or Bellman-Ford, we can find the shortest path between any two given pairs of nodes.
In order to keep track of the shortest path between any two given nodes, these algorithms employ a three-dimensional array. Also, in order to keep track of how far they are from the starting point, they compare the result to the distance between the starting point and the intermediate node at each stage. After all, iterations are complete, the final solution will be the distance matrix.
There are several uses for solving the all-pair shortest path issue, such as in network analysis, routing, navigation, social network analysis, etc.
#3. Seam Carving
In the field of image processing, seam carving is an intriguing application of dynamic programming. The task at hand is to reduce the size of an image without altering any of its essential characteristics. Low-energy routes in an image, known as seams, can be used to subtract or add pixels to achieve this effect.
Using dynamic programming, we can calculate the cumulative energy of each pixel in the image based on its gradient and neighbors, and then utilize that information to determine which seams should be removed or added. Then, by working our way up from the bottom of the picture, we may locate the seam with the least amount of potential energy. This method can be used again until the required size is achieved.
In addition, images can be resized, cropped, retargeted, and more with the help of seam carving.
#4. Machine Learning and Genomics
Machine learning and genomics challenges like sequence alignment, hidden Markov models, and phylogenetic trees are all amenable to dynamic programming’s problem-solving abilities.
Aligning multiple sequences of symbols (often DNA or proteins) to uncover commonalities is called sequence alignment. This can shed light on their evolutionary linkages, functions in society, or structural characteristics. Optimal alignments can be found via dynamic programming by assigning scores to matches and mismatches between sequences.
Probabilistic models known as Hidden Markov models are used to describe time series data that is conditional on unknown states. They are useful for modeling difficult phenomena like speech recognition, NLP, bioinformatics, etc. When given a set of observations, dynamic programming techniques like Viterbi and Forward-Backward can determine the most likely sequence of hidden states.
Phylogenetic trees show the connections between species or genes over time. It is possible to infer common ancestors, dates of divergence, and evolutionary events from these commonalities. Also, a dynamic programming algorithm like Fitch and Sankoff can be used to generate optimal phylogenetic trees using sequencing data.
#5. Cryptography
Cryptography, the study of secret communication, also benefits from dynamic programming’s problem-solving abilities. Encryption, decryption, digital signatures, authentication, and other similar processes are all part of cryptography.
Encryption converts information from human-readable to secret-key-readable. Decryption is the process of converting encrypted data back into plaintext using the original key or a new one. Digital signatures allow for the verification of the authenticity and integrity of a message or document. Checking the credentials of either the sender or the receiver can verify the sender’s or receiver’s identity.
Different types of cryptography, including dynamic key cryptography, code-based cryptography, and dynamic programming-based cryptography, can all be implemented with dynamic programming.
Dynamic key cryptography is a mechanism for encrypting and decrypting messages with constantly changing keys. Keys that are “dynamic” are ones that evolve over time or in response to other factors. This makes them more secure than static keys, which are vulnerable to attacks. It is possible to use dynamic programming to generate and keep keys up to date when implementing dynamic key cryptography.
Using a technique known as code-based cryptography, it is possible to encrypt and decrypt messages by employing error-correcting codes in the process of doing so. It is possible to fix transmission faults with error-correcting codes. The use of code-based cryptography is widely regarded as quantum-resistant since it is secure against assaults from quantum computers. Dynamic programming can be used to encipher and decipher communications using a code-based cryptosystem.
As a method for encrypting and decrypting data, dynamic programming-based cryptography relies on a dynamic programming algorithm. In order to tackle optimization challenges, dynamic programming techniques typically partition the problem into a set of simpler subproblems. Dynamic programming cryptography uses knapsack, shortest path, and seam carving.
What Is a Real World Example of Dynamic Programming?
Numerous instances of real-world software applications use dynamic programming to maintain agility and efficiency while reducing their resource footprint on the host system. Some instances are as follows:
- Google Maps. Google Maps uses dynamic programming to find the quickest route from a given origin to several different destinations.
- Networking. Sequential data transfer from a single sender to multiple recipients.
- Spell checkers. The edit distance algorithm determines the number of steps needed to transform one word into another and provides a quantitative measure of the degree of dissimilarity between the two words.
- Plagiarism software. Document distance methods assist determine text document similarity.
- Search engines. To determine how similar two pieces of internet content actually are.
How to Solve Dynamic Programming Problems?
Learning the formula for resolving dynamic programming problems is the next step after understanding the concept of dynamic programming. Here are a few suggestions for how to apply dynamic programming to the problem at hand and arrive at a workable solution:
#1. Acknowledge the Dynamic Programming Issue
The most important part is realizing that a dynamic programming algorithm can solve the specified problem statement. Solving this problem requires first determining if each of the problem statements can be split down into smaller parts as a function.
#2. Determine the Causes of the Issue
If you’ve already concluded that dynamic programming is the right tool for the job, the next step is to identify the problem’s recursive structure among its constituent subproblems. In this case, you must account for the fluid nature of the problem’s conditions. This variable could be an array position or problem resolution speed.
In addition, counting the problem’s constituent parts is crucial.
#3. Choose Between an Iterative and a Recursive Method
To fix dynamic programming problems, you can utilize iterative or recursive approaches. From what has been said thus far, it’s safe to say that the recursive method is preferable. All of the aforementioned considerations, however, stand on their own, regardless of the method chosen to solve the problem.
Both the recursive and iterative approaches need you to specify the recurrence relation and the base case of the problem.
#4. Incorporate a Memorization System
When tackling an issue with a similar structure, it can be helpful to recall past experience handling comparable subproblems. The problem’s time complexity will decrease as a result of this. The time complexity of a task might grow exponentially if we keep solving the same subproblems over and over again without using memorization.
#5. Put the Recurrence Relation Into Words
When solving a problem, many programmers skip over defining the recurrence relation and jump straight to coding. You’ll have a better grasp of the problem and be able to code it more quickly if you can express the recurrence relation explicitly before you start.
Algorithm Dynamic Programming
Most applications of dynamic programming include the recursive algorithm. The use of dynamic programming for optimization implies that recursion is intrinsic to the majority of optimization issues.
However, it is not possible to solve all-recursive problems with dynamic programming. A recursion can only find the solution by a divide and conquer strategy unless there is a presence of overlapping subproblems, as in the Fibonacci sequence problem.
This is because the underlying subproblems in a recursive algorithm like Merge Sort do not overlap, ruling out the use of Dynamic Programming.
Different Types of Dynamic Programming Algorithms
Here are the different types of dynamic programming algorithms.
#1. Longest Common Subsequence
It is possible for the elements of the longest common subsequence (LCS) to appear in any order within the original sequences; the LCS is defined as the longest subsequence that is common to all the specified sequences.
If two sequences S1 and S2 are provided, then a sequence Z that is a subsequence of both S1 and S2 is called their common subsequence. As an added requirement, Z must consist of a strictly ascending sequence of the indices of sets S1 and S2.
The selected elements’ indices in Z must increase strictly in order to form a rising sequence.
#2. Floyd-Warshall Algorithm
Finding the shortest path between every pair of vertices in a weighted graph is the goal of the Floyd-Warshall Algorithm. This method processes charts with weights in both directions. On the other hand, it fails for cycles in which the sum of their edges is negative.
Floyd’s algorithm, Roy-Floyd algorithm, Roy-Warhshall algorithm, and WFI algorithm are all names for the Floyd-Warhshall algorithm.
This algorithm uses a dynamic programming technique to locate optimal shortcuts.
How Does a Dynamic Programming Algorithm Solve Lcs Problems Faster Than a Recursive Technique?
Dynamic programming reduces the overhead of calling a function. It remembers the outcome of each function call so that subsequent calls can make use of the stored data without repeating the same work.
Every time an element of X is compared to an element of Y, the results are written to a table so that they can be used in subsequent calculations in the aforementioned dynamic process.
Therefore, a dynamic method’s runtime is the same as the time needed to fill the table (O(mn)). In contrast, the complexity of the recursive algorithm is 2max(m, n). Also, read How to Choose the Right Type of Encryption Algorithm for Your Business Needs
What Are the Dynamic Programming Problems in Python
Utilizing dynamic programming, one can determine the most appropriate solution to any number of different problem statements. In the following, we will go over some of the most frequently requested famous problem statements and provide a brief explanation along with the appropriate Python code.
#1. Knapsack (0-1) Bounded
In this situation, you are given the prices and weights of N goods and tasked with fitting them into a backpack of capacity W; the goal is to minimize the number of items chosen while still fitting everything in the knapsack.
Most technical interviews for goods organizations will require candidates to solve the knapsack problem, which is a classic example of a dynamic programming technique.
Statement of the Problem Assume that you have a bag with capacity W and a list of things, each of which has a weight and corresponding profit. The goal is to maximize earnings by effective bad filling.
The answer is to make a table with columns for each conceivable weight between 1 and W and rows for the weights you actually select. This table is going to be known as dp[][]. If ‘j’ is the knapsack’s capacity and the first ‘i’ elements in the weight/item array are included, then the state /cell dp[i][j] in the table indicates the highest possible profit.
As a result, the value in the final cell will signify the solution. It’s important to pack only what won’t exceed the knapsack’s weight restriction. There are two alternatives to the criterion “weight>wt[i-1]” where all columns can be filled.
#2. 0/1 Knapsack Bounded Memoization
Fill a bag with items of known weight and profit, size K. Your goal is to maximize your earnings. Here, we’ll use memoization instead of tabulation to see whether we can solve the problem.
The above 0/1 knapsack problem employed a bottom-up strategy to discover a solution, whereas this problem uses a top-down approach based on memorization to obtain a solution.
Dynamic programming uses memorization to reduce the need to solve the same parts of the issue several times. This eliminates the need to constantly solve the sub-problem and streamlines the process of generating output.
Statement of the Problem Assume that you have a bag with capacity W and a list of things, each of which has a weight and corresponding profit. If the bag is full with as much efficiency as feasible, one can get the highest potential level of profit.
The solution is to first construct a two-dimensional array to hold the final answers to the individual subproblems. The table’s columns will list all potential weights between 1 and W, partitioning it into that many sections, and the rows will show the weights you select at each given time.
We use a dp array to keep track of each solved subproblem. Rather than resolving a previously solved subproblem, we just return its answer.
#3. Equal Subset Problem
Find a partition of the given set such that the total of items in both subsets is the same using dynamic programming to solve the equal subset issue. In addition to its other names, the equal subset issue (or partition problem) is a prime illustration of the power of dynamic programming.
The task at hand requires us to divide the array arr in half so that each of the ensuing subsets has the same overall size.
As a solution, we need to build a two-dimensional array with dimensions of (sum/2+1)*(target+1). Here, the results of splitting the original array can be stored for each subset and each sum, and later retrieved. The array’s first dimension will represent the various subsets that can be created, while the array’s second dimension will represent the various sums that can be calculated by combining subsets.
Advantages of Dynamic Programming
Here are some of the advantages of dynamic programming.
#1. Effective Remedy
Dynamic programming is a powerful tool for finding optimal solutions to issues with optimal substructure and overlapping sub-problems. By decomposing them into manageable pieces, these challenges are easier to tackle with the method. Dynamic Programming is able to create an optimal solution by avoiding repetitive calculations and reusing answers to sub-problems.
#2. Facilitates Easy Problem-Finding
Solving a difficult problem can be easier by first decomposing it into simpler parts. It makes complex problems easier to tackle by partitioning them into more manageable chunks. This method simplifies the solution and makes the problem more accessible.
#3. Efficient
By eliminating unnecessary computations and recycling previously solved subproblems, Dynamic Programming can significantly cut down on the time required to solve a problem. When the sub-problems overlap, the method can help by reducing the total number of measures required to resolve the issue.
#4. Effective When a Problem Has Multiple Solutions
Dynamic Programming can help determine which of several possible explanations is more likely to be the case. When there are several viable options for fixing an issue, this method can help us zero in on the best one.
What Are the Drawbacks of Dynamic Programming?
Here are some of the disadvantages of dynamic programming.
#1. Sub-issues That Keep Recurring
Dynamic programming works best when the problem has overlapping sub-problems, which may not always be the case. It’s not going to work, and it probably won’t provide you the best solution, if the individual problems don’t intersect.
#2. Complicacy in Time and Space
If the problem is large, Dynamic Programming may require a lot of memory and storage space, which increases the time and space complexity of the solution. Using memory, the approach stores interim results in a table or a memoization table.
#3. Framework for the Issue
Although effective for certain problem structures, Dynamic Programming is not always the best choice. This method works best when the problem has overlapping sub-problems, hence it may not be applicable to other situations.
#4. Difficult to put into practice
Dynamic programming needs an in-depth knowledge of algorithms and data structures, making it challenging to implement for beginners. The method necessitates prior thought and in-depth familiarity with the issue at hand.
Bottom Line
In conclusion, Dynamic Programming is an effective method for finding answers, although other approaches are preferable. It is crucial to know the pros and cons and pick the right method according to the issue at hand. For problems with optimal substructure and overlapping sub-problems, Dynamic Programming can yield an optimal solution; however, this method may not always be applicable.
Although it is difficult to develop and uses a lot of memory, its ability to streamline the problem-solving process and shorten computation times makes it a significant resource for computer scientists and mathematicians.
Dynamic Programming FAQs
What Is the Difference Between Linear Programming and Dynamic Programming?
For linear optimization problems, we have the linear programming (LP) algorithm, and for generic nonlinear optimization problems with non-convex constraints, we have dynamic programming (DP), which guarantees the global optimality of a solution.
How Hard Is It to Learn Dynamic Programming?
It’s common knowledge that dynamic programming is a complex subject, especially for newcomers to the field of computer science. However, one may learn dynamic programming with ease with a firm grasp of foundational principles and ample practice.
Is Dynamic Programming Very Hard?
They’re hard! To start, the idea of dynamic programming methods can be difficult to grasp. Any expert programmer would attest that mastery of DP requires a significant time commitment. The skill of decomposing a problem into its constituent parts and reassembling it into a workable whole is also necessary.
Similar Articles
- PROJECT TIME MANAGEMENT: Processes, Tools & Software for Effective Management
- AMAZON SEO: How To Optimize Your Products To Rank Better
- MOST POPULAR PROGRAMMING LANGUAGES: 2023 Guide
- WHAT IS COMPUTER PROGRAMMING: Examples, Types, Courses & Software
- Wills Online: Best Online Will Makers.